GO Ontology Relations

The occurs in relationship

The occurs in relation is used to specify the location in which a biological process or a molecular function takes place. Whereas part of and has part are used to link two entities (cellular components) or two occurrents (functions or processes), occurs in is used for linking an occurrent—a function or process—to a location. As with part of and has part, a relationship is only created if the process always occurs in that location, i.e. process A necessarily occurs in component B. If process A occurs, component B must exist; however, if component B exists, we cannot say for certain that process A occurs.

Many of the process terms linked by occurs in relations mention the location in the term name.

i.e. all process A occur in B; some B are the location of occurrence of A.

For example:

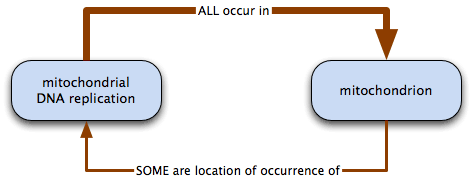
mitochondrial DNA replication necessarily occurs in mitochondrion: all mitochondrial DNA replication takes place in some mitochondria; some mitochondria are the location of mitochondrial DNA replication.

Reasoning over occurs in

occurs in is a → occurs in

If A occurs in B, and B is a C, A occurs in C. For example:

mitochondrial DNA replication occurs in mitochondrion, and mitochondrion is a intracellular membrane-bounded organelle
therefore mitochondrial DNA replication occurs in intracellular membrane-bounded organelle

is a occurs in → occurs in

If the order of the relationships is reversed, the result is the same; if A is a B, and B occurs in C, A occurs in C.

For example:

mitochondrial DNA repair is a mitochondrial DNA metabolic process and mitochondrial DNA metabolic process occurs in mitochondrion
therefore mitochondrial DNA repair occurs in mitochondrion

occurs in part of → occurs in

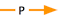
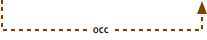
For example:

mitochondrial DNA replication occurs in mitochondrion and mitochondrion part of cell
therefore mitochondrial DNA replication occurs in mitochondrion

part of occurs in → occurs in

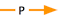
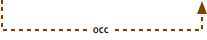
For example:

transcription elongation from mitochondrial promoter part of termination of mitochondrial transcription and termination of mitochondrial transcription occurs in mitochondrion
therefore transcription elongation from mitochondrial promoter occurs in mitochondrion

occurs in has part → no inference

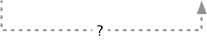
has part occurs in → partially occurs in

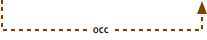
For example:

has part and occurs in
therefore partially occurs in

has part AND occurs in

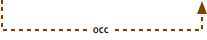
This situation is where the term B has both a has part child and an occurs in child. Process A is a necessary subprocess of B, so we can infer that because B occurs in C, A must occur in C.

occurs in regulates → INVALID

The subject of a regulates relationship—the activity that does the regulating—must be an occurrent, not an entity; therefore the object of an occurs in relationship, which must always be an entity, cannot be the subject of a regulates relationship. The same applies for positively regulates and negatively regulates.

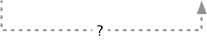
regulates occurs in → ???

We cannot make an inference

Back to top

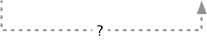
Gene Product Relations

In addition to specifying relations between terms, we can also name the relationships between gene products and terms. Informally, we say "gene product X is annotated to term Y", but it can be stated more precisely using the relations localizes to and has function in.

Note that these relations are only used to describe the connection between a gene product and an ontology term.

Back to top

The localizes to relation

localizes to describes the relationship of a gene product to a cellular component; for example: gene product X localizes to cell membrane; gene product Y localizes to phosphopyruvate hydratase complex

localizes to is only used for terms in the cellular component ontology.

Reasoning over localizes to

Just as we can infer relationships between terms, we can also combine the relationship between a gene product and a term with those of the term to its ancestors. As with inference of relations between terms, we proceed iteratively through the ontology, following the direction of the relationships.

localizes to is a → localizes to

localizes to is transitive over is a, so we can infer that any gene product that localizes to a certain cellular component also localizes to all is a ancestors of the term. For example, knowing a gene product that localizes to a mitochondrion, which is an organelle, allows us to infer that it localizes to an organelle.

localizes to part of → localizes to

localizes to is also transitive over part of; a gene product that localizes to a cellular component also localizes to all is a ancestors of the term. In the example below, mitochondrion is part of the cytoplasm, so the gene product localizes to the cytoplasm.

localizes to localizes to → INVALID

Note that because the subject of the localizes to relationship (i.e. the X in the statement ‘X localizes to Y’) must be a gene product and the object (Y) must be a cellular component term, the combination of two localizes to relationships would not occur with the set of relationships currently used in the Gene Ontology. Similarly, localizes to would not be combined with has function in relationships would not occur with the set of relationships currently used in the Gene Ontology.

localizes to regulates → INVALID

Cellular component terms represent locations, and as such cannot have a regulates relationship with other terms.

Back to top

The has function in relation

A gene product has function in a biological process or a molecular function. For example:

• xxx has function in homeostasis
• xxx has function in regulation of cell size
• xxx has function in UDP-glucose 6-dehydrogenase activity

has function in is only used for terms in the biological process and molecular function ontologies.

Reasoning over has function in

has function in is a → has function in

has function in is transitive over is a, and a gene product that has function in a biological process or molecular function has function in all the is a ancestors of that process or function. In the example, mitotic telophase is a cell cycle phase, so we can infer that a gene product annotated to mitotic telophase has function in a cell cycle phase.

has function in part of → has function in

has function in is also transitive over part of; mitotic telophase is part of mitosis, and a gene product annotated to mitotic telophase has function in mitosis.

has function in regulates → regulator of

Combining a has function in relation with regulates results in a regulator of relationship; for example, a gene product that has function in regulation of mitosis, which regulates mitosis would be a regulator of mitosis.

Similarly, a gene product that has function in a process that positively regulates or negatively regulates a second process is a positive regulator of or negative regulator of the second process.

Back to top

Annotation Relationship Summary

localizes to

• →
• →

has function in

• →
• →
• →
• →
• →

Back to top

Annotations and other relationships

Problems with inferring over localizes to

The relationship between gene products and classes in the cellular component ontology is localizes to. Its usage is such that it means some gene product X localize to some cellular component.

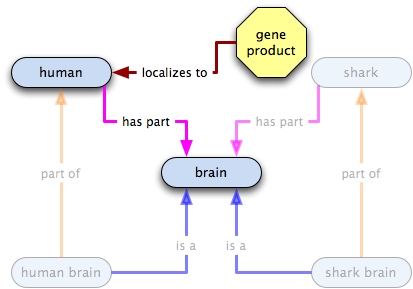
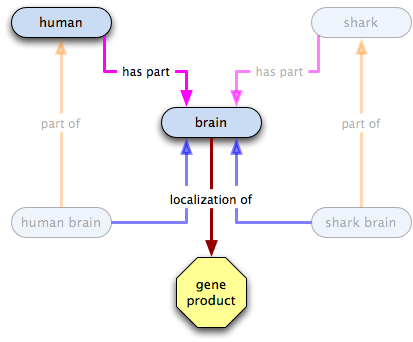
Set up: we have the above ontology, and we want to annotate two gene products; one is a neuronal GP, and the other is a GP from the hippocampus. Both sharks and humans have neurons in their brains, but Wikipedia reliably informs me that only mammals have a hippocampus, so the poor old sharks are bereft of the second gene product.

This would be the ontology structure with inferred relations if we were to use the standard GO practice of creating specific child terms.

Annotating the neuronal GP

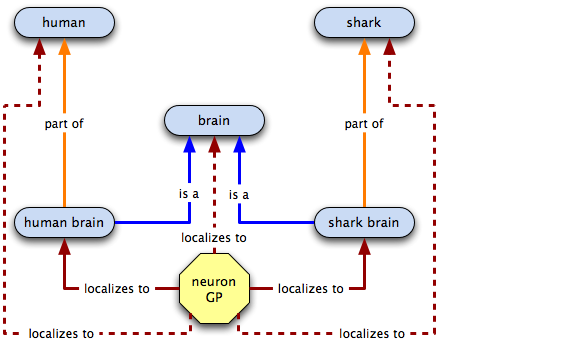
Annotating the hippocampus GP

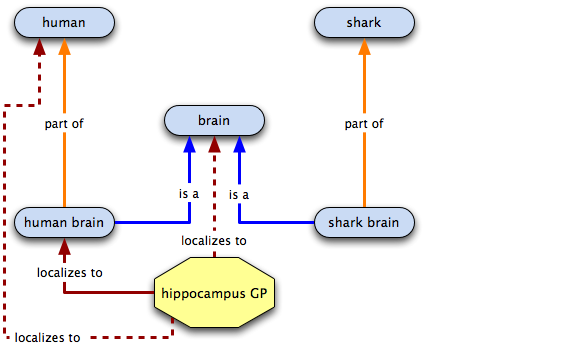
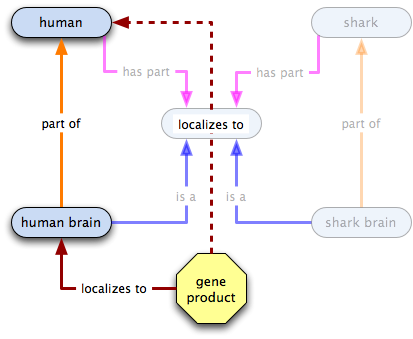
In the spirit of global cutbacks, we want to get rid of those extra terms, so we make has part links and do away with the old terms.

Let's see what we can infer from the graph now. Here's the neuronal GP:

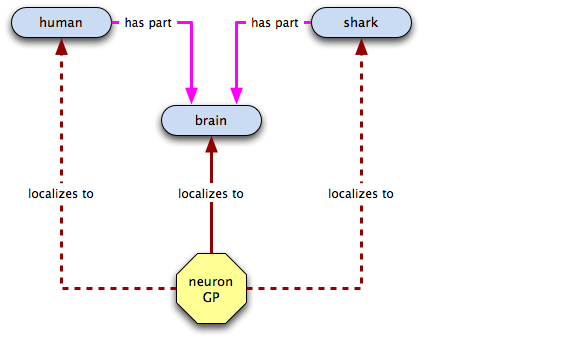
So far so good... now let's check out the hippocampus GP

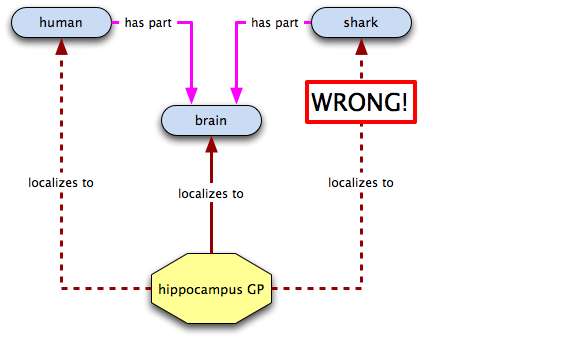
Oh crap! Now what do we do?! It turns out that we probably shouldn't have inferred that localized to was transitive over has part. We do still want to be able to capture the fact that the hippocampus GP localizes to humans, though. How can we do that? Well, how about a relation that states that in a certain species—humans, in this case—a certain class always has certain annotatable entity in it? Or, to say that in English, why not say that the neuronal GP is integral to brains, i.e. an all-some localization relation from brain to the neuronal GP? Let's give it a go:

Not bad. Let's check out our finished graph:

As you can see, this method of representation loses us the hippocampus-brain connection, but if sharks don't need 'em, nor do we!

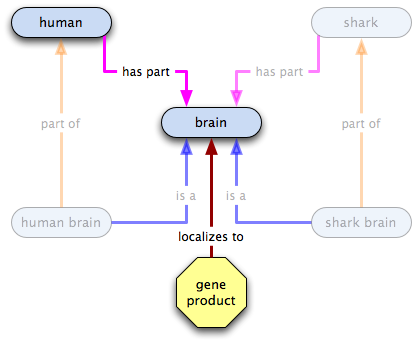
localizes to

The relationship between gene products and classes in the cellular component ontology is localizes to. Its usage is such that it means some gene product X localize to some cellular component.

is a

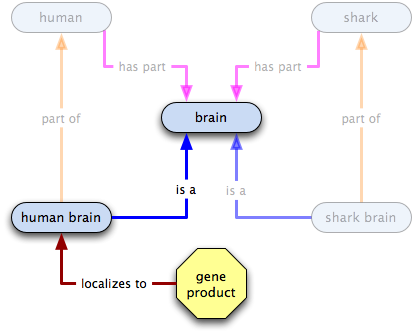
Given this statement:

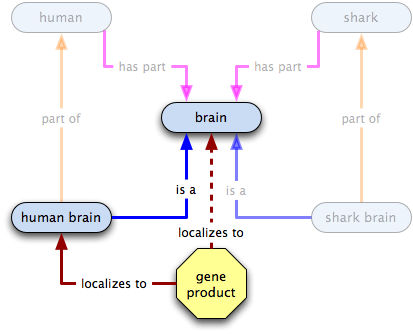
gene product X human brain brain

what do we know?

• some instances of X localize to some human brains
• all human brains are a type of brain
• therefore some Xs localize to some brains
• some human brains, and therefore some brains, have Xs localized in them
• the existence of human brains or of brains does not imply the existence of X
• the existence of X does not imply the existence of human brains or brains

Inferences:

part of

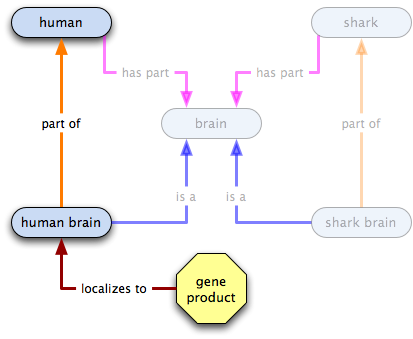
gene product X human brain human

• all human brains are part of some human, so the existence of human brains implies the existence of humans
• some Xs localize to some human brains, so some Xs localize to some humans
• some human brains, and therefore some humans, have Xs localized in them
• the existence of human brains or of humans does not imply the existence of X
• the existence of X does not imply the existence of human brains or humans

Inferences:

has part

gene product X human brain

• all humans have some brains as a part [theoretically, anyway]
• some brains are part of humans, but in an open world (such as that in which we do GO), we cannot infer the existence of humans from the brains as the brains may be part of other entities (e.g. sharks)
• the existence of X does not imply the existence of humans or of brains
• however, an instance of X localized to humans implies that humans exist, and therefore brains exist
• we cannot infer where the gene product localizes to from the current graph

gene product X brain
human brain

• all humans have some brains as a part; if humans exist, brains exist
• the existence of brains does not imply the existence of humans
• the existence of X does not imply the existence of humans or of brains
• an instance of the localization of X to brains means that brains exist, but we cannot be sure that humans exist

localized in (integral to)

More powerful reasoning can be accomplished by stating that gene product X is integral to cellular component Y, i.e. all cellular component Y have some X localized in them. Now our annotations make the following statements:

• SOME gene product X localizes to cellular component Y
• ALL cellular component Y have SOME gene product X localized in them

is a

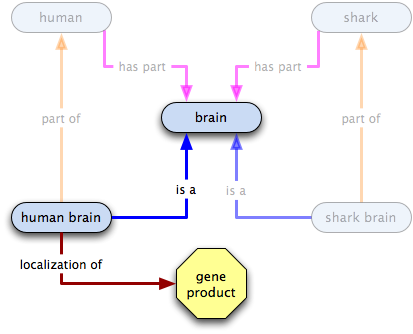
• some instances of X localize to some human brain
• all human brains are a type of brain
• therefore some Xs localize to some brains
• all human brains have X localized in them
• some brains have X localized in them
• the existence of human brains implies the existence of X
• the existence of brains does not imply the existence of X (might not be any human brains)
• the existence of X does not imply the existence of human brains or brains

part of

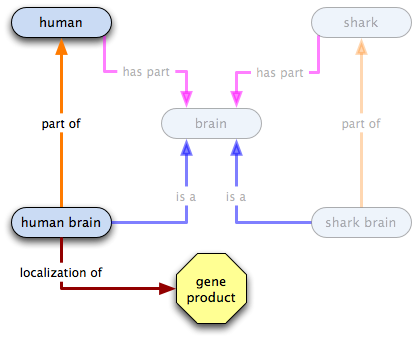
• all human brains are part of some human, so the existence of human brains implies the existence of humans
• some Xs localize to some human brains, so some Xs localize to some humans
• all human brains have X localized to them, therefore so do all humans
• the existence of human brains implies the existence of X
• the existence of humans implies the existence of X
• the existence of X does not imply the existence of human brains or humans

has part

• all humans have some brains as a part
• all humans have some X localized in them
• the existence of humans implies the existence of brains and of X
• the existence of X does not imply the existence of humans
• the existence of brains does not imply the existence of humans
• an instance of X localized in a human implies the existence of humans and brains

• all humans have some brains as a part
• all brains have some X localized in them; the existence of brains implies the existence of X
• therefore all humans have X localized in them; the existence of humans implies the existence of brains and of X
• the existence of X does not imply the existence of humans or of brains

Back to top